A total of 5820 evaluation scores from Gazi University students in Ankara, Turkey, are included in this data collection. There are an extra five qualities in addition to a total of 28 course-specific questions. Here we are going to perform Turkiye Student Evaluation clustering analysis by three clustering algorithms.
We will apply following machine learning algorithms
- K-Means Clustering
- Agglomerative Hierarchical Clustering
- DBSCAN Clustering
Dataset used for this project from kaggle website. Here the link Turkiye Student Evaluation Analysis.
Variables information

Importing Libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans, AgglomerativeClustering, DBSCAN
from sklearn.metrics import silhouette_score
from scipy.cluster.hierarchy import dendrogram, linkage
from IPython.display import displayLoad the Dataset
dt = pd.read_csv("turkiye-student-evaluation_generic.csv")
dt.head()
dt.describe()
dt.info()
dt.isnull().sum()
Exploratory data analysis
You can follow Exploratory data analysis article to get detailed information about it.
Distribution of Categorical Variables
# Distribution of Categorical Variables
plt.figure(figsize=(15, 6))
sns.countplot(x = dt['instr'] , data = dt)
plt.title('Distribution of Instructors')
plt.show()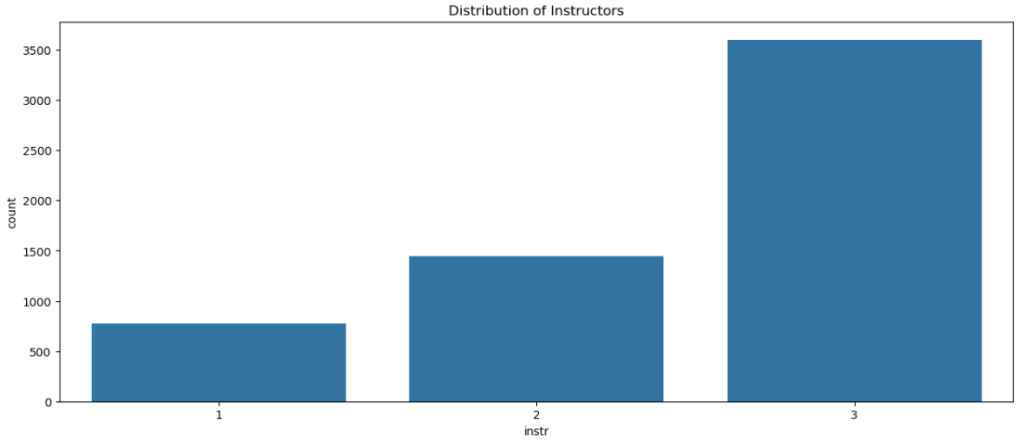
plt.figure(figsize=(15, 6))
sns.countplot(x = dt['class'] , data = dt)
plt.title('Distribution of class')
plt.show()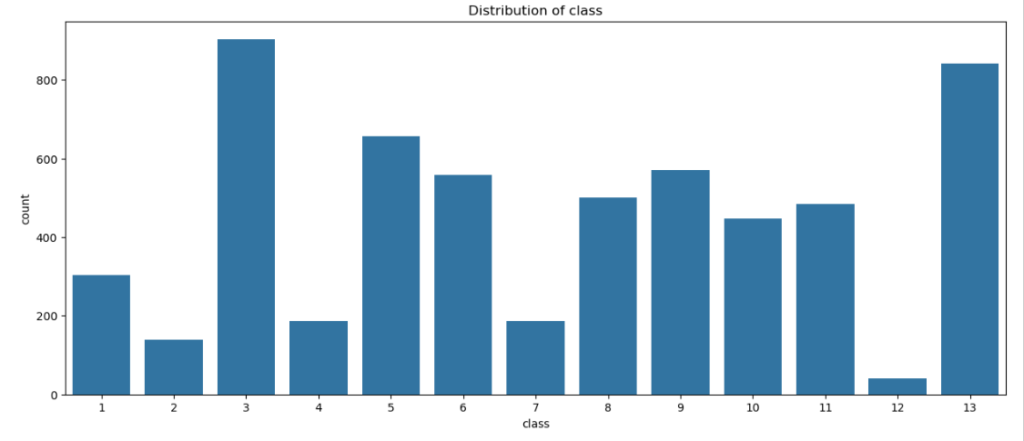
plt.figure(figsize=(15, 6))
sns.countplot(x = dt['attendance'] , data = dt)
plt.title('Distribution of attendance')
plt.show()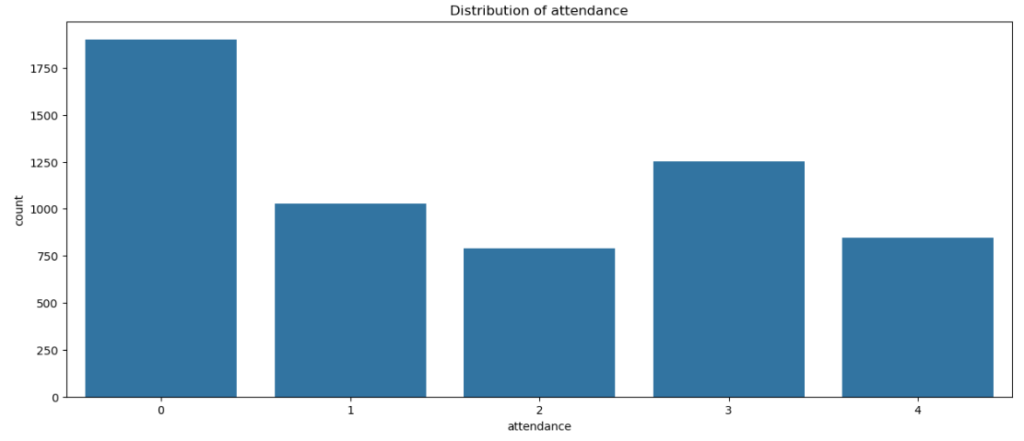
plt.figure(figsize=(15, 6))
sns.countplot(x = dt['difficulty'] , data = dt)
plt.title('Distribution of difficulty')
plt.show()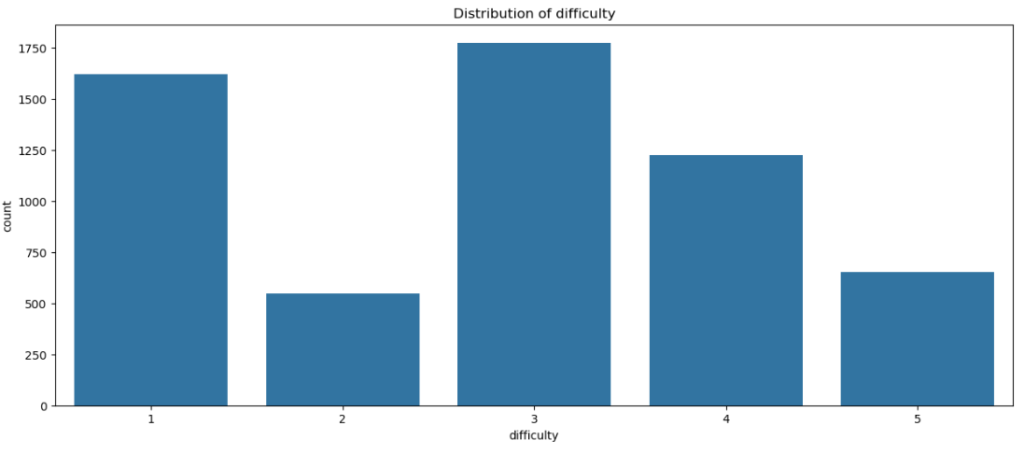
Correlation Analysis
plt.figure(figsize=(18, 12))
sns.heatmap(dt.iloc[:, 5:].corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix of Questions')
plt.show()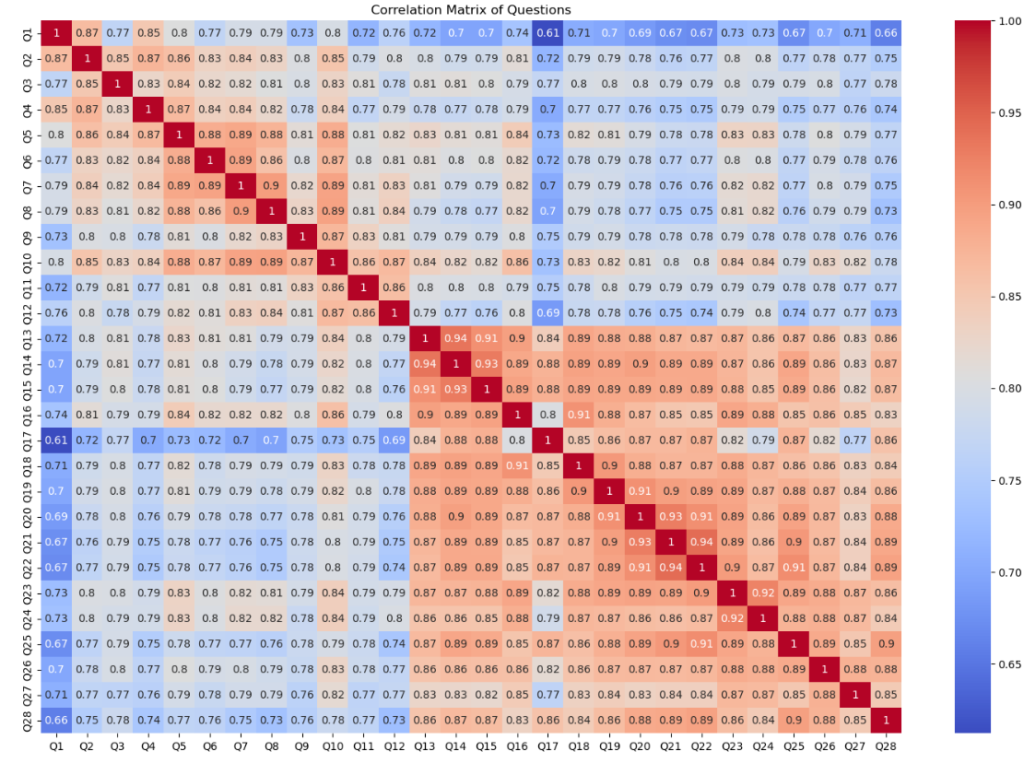
Dropping columns
X = dt.drop(columns=['instr', 'class', 'nb.repeat', 'attendance', 'difficulty'])
X.columns
Apply Standard Scaler on Variable X
sc = StandardScaler()
x_SC = sc.fit_transform(X)Apply PCA for Dimensionality Reduction
X variable contains 28 columns so are going to apply PCA to reduce the columns
pca = PCA(n_components = 2)
x_pca = pca.fit_transform(x_SC)# Explained variance to understand how much variance is captured
explained_variance = pca.explained_variance_ratio_
print(f"Explained variance by PCA components: {explained_variance}")Explained variance by PCA components: [0.82288939 0.04474705]
Elbow Method for Optimal K
For clustering we have to find K value by Elbow method
wcss = []
K_range = range(1, 15)
for k in K_range:
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(x_pca)
wcss.append(kmeans.inertia_)# Plotting the Elbow Curve
plt.figure(figsize=(10, 6))
plt.plot(K_range, wcss, 'bo-')
plt.title('Elbow Method For Optimal K (PCA Data)')
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Within-Cluster Sum of Squares (WCSS)')
plt.xticks(K_range)
plt.show()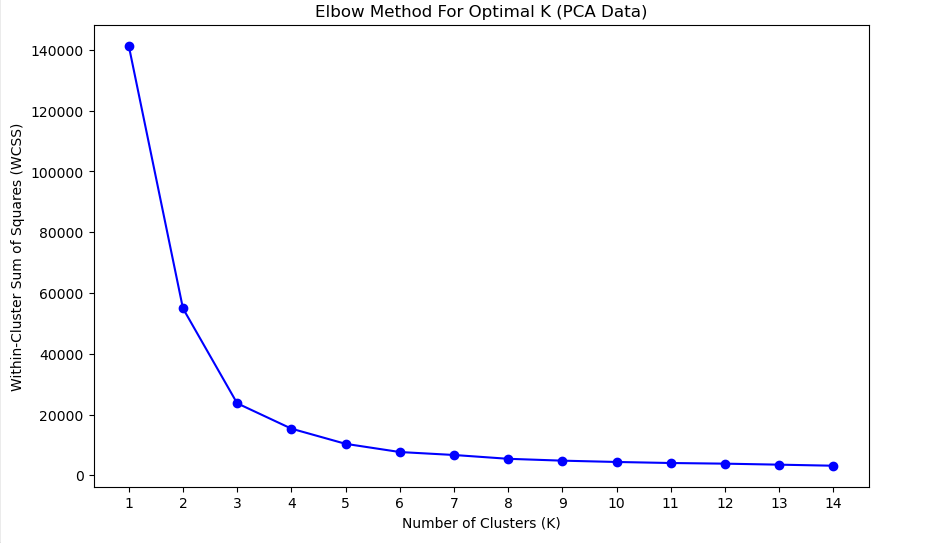
optimal_k = 3K-Means Clustering
kmeans = KMeans(n_clusters=optimal_k, random_state=42)
kmeans_labels = kmeans.fit_predict(x_pca)
silhouette_kmeans = silhouette_score(x_pca, kmeans_labels)
print(f'K-Means Silhouette Score with {optimal_k} clusters: {silhouette_kmeans}')K-Means Silhouette Score with 3 clusters: 0.5740803780073331
Visualizing K-Means Clusters
# Visualizing K-Means Clusters
plt.figure(figsize=(10, 6))
plt.scatter(x_pca[:, 0], x_pca[:, 1], c=kmeans_labels, cmap='viridis', marker='o')
plt.title(f'K-Means Clusters (K={optimal_k}) with PCA')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()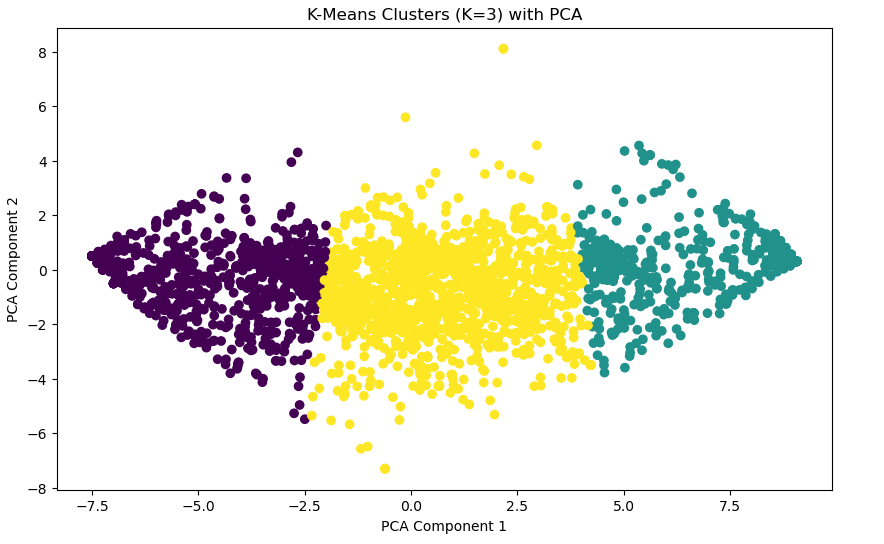
Agglomerative Clustering
Dendrogram to find k value
plt.figure(figsize=(10, 6))
Z = linkage(x_pca, 'ward')
dendrogram(Z)
plt.title('Dendrogram of Agglomerative Clustering')
plt.xlabel('Samples')
plt.ylabel('Distance')
plt.show()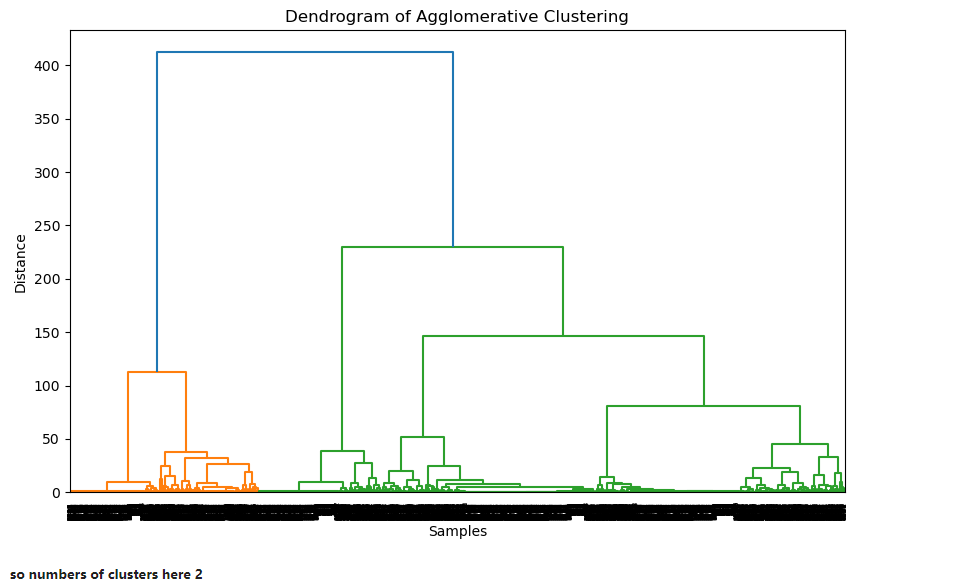
agg_cluster = AgglomerativeClustering(n_clusters=2)
agg_labels = agg_cluster.fit_predict(x_pca)
silhouette_agg = silhouette_score(x_pca, agg_labels)
print(f'Agglomerative Clustering Silhouette Score: {silhouette_agg}')
Agglomerative Clustering Silhouette Score: 0.5608549603760143
# Visualizing Agglomerative Clustering Clusters
plt.figure(figsize=(10, 6))
plt.scatter(x_pca[:, 0], x_pca[:, 1], c=agg_labels, cmap='plasma', marker='o')
plt.title(f'Agglomerative Clustering (K={2}) with PCA')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()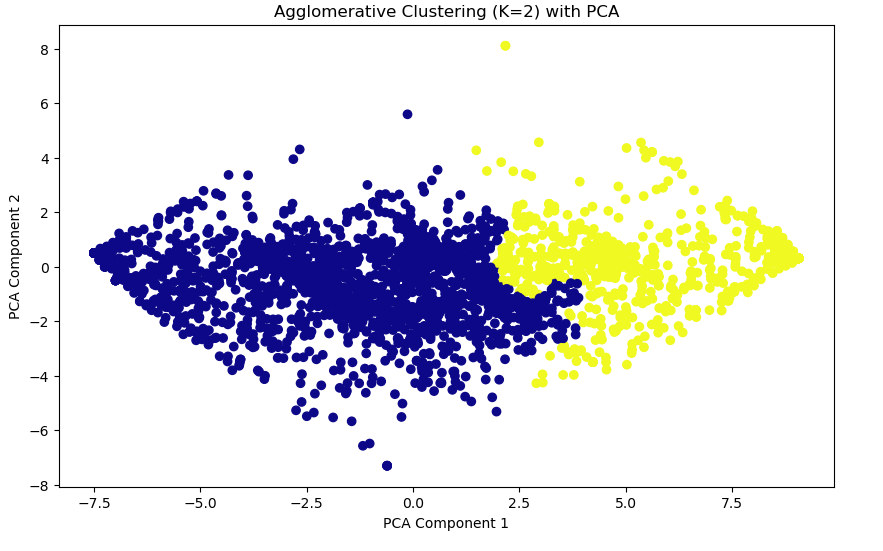
DBSCAN Clustering
dbscan = DBSCAN(eps=0.5, min_samples=5)
dbscan_labels = dbscan.fit_predict(x_pca)
# Exclude noise (-1 label) when calculating silhouette score for DBSCAN
if len(set(dbscan_labels)) > 1: # Ensure there are more than 1 cluster
silhouette_dbscan = silhouette_score(x_pca[dbscan_labels != -1], dbscan_labels[dbscan_labels != -1])
print(f'DBSCAN Silhouette Score: {silhouette_dbscan}')
else:
silhouette_dbscan = "DBSCAN didn't form distinct clusters."
print(silhouette_dbscan)DBSCAN Silhouette Score: -0.08714974885925647
# Visualizing DBSCAN Clusters
plt.figure(figsize=(10, 6))
plt.scatter(x_pca[:, 0], x_pca[:, 1], c=dbscan_labels, cmap='inferno', marker='o')
plt.title('DBSCAN Clusters with PCA')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()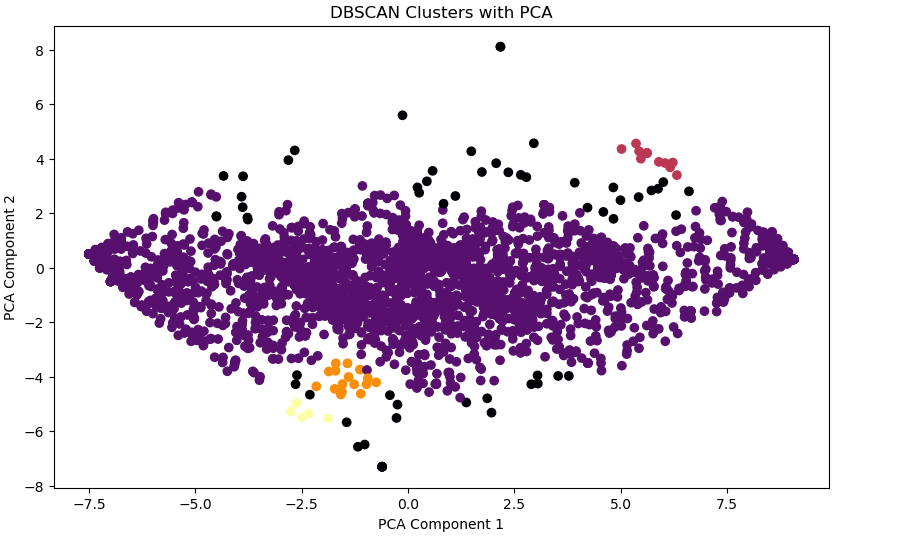
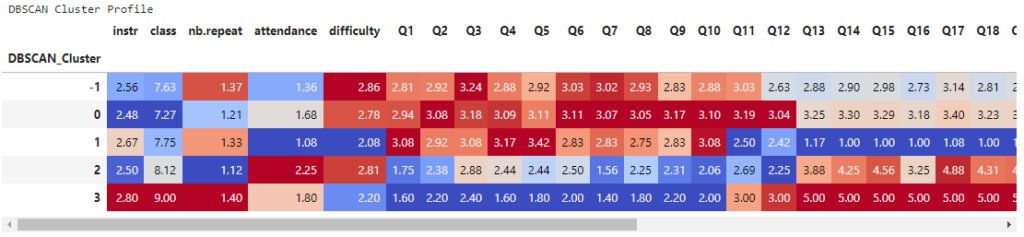
Interpretation – Cluster Profiles
# Add cluster labels to the original data
dt['KMeans_Cluster'] = kmeans_labels
dt['Agglomerative_Cluster'] = agg_labels
dt['DBSCAN_Cluster'] = dbscan_labels# Analyze clusters
kmeans_profile = dt.groupby('KMeans_Cluster').mean()
agg_profile = dt.groupby('Agglomerative_Cluster').mean()
dbscan_profile = dt.groupby('DBSCAN_Cluster').mean()Define a function to style DataFrames for better readability
def style_clusters(df):
return df.style.background_gradient(cmap='coolwarm').format(precision=2)# Display the cluster profiles
print("KMeans Cluster Profile")
display(style_clusters(kmeans_profile))

print("Agglomerative Cluster Profile")
display(style_clusters(agg_profile))
print("DBSCAN Cluster Profile")
display(style_clusters(dbscan_profile))